The 2-summing norm of 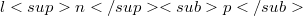 computed with n vectors
computed with n vectors
Abstract
The 2-summing norm of an n-dimensional Banach space computed with n vectors is known to belong between 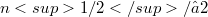 and
and 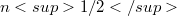 . It is shown that the 2-summing norm of real
. It is shown that the 2-summing norm of real 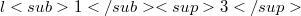 computed with three vectors is 5/3. Some lower estimates for 2-summing norms of
computed with three vectors is 5/3. Some lower estimates for 2-summing norms of 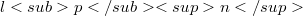 computed with n vectors are stated, which are considerably better than universal ones and are based on the existence of certain block designs or Hadamard matrices.
computed with n vectors are stated, which are considerably better than universal ones and are based on the existence of certain block designs or Hadamard matrices.
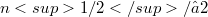 and
and 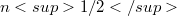 . It is shown that the 2-summing norm of real
. It is shown that the 2-summing norm of real 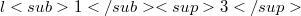 computed with three vectors is 5/3. Some lower estimates for 2-summing norms of
computed with three vectors is 5/3. Some lower estimates for 2-summing norms of 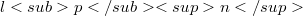 computed with n vectors are stated, which are considerably better than universal ones and are based on the existence of certain block designs or Hadamard matrices.
computed with n vectors are stated, which are considerably better than universal ones and are based on the existence of certain block designs or Hadamard matrices.DOI Code:
10.1285/i15900932v14n1p81
Full Text: PDF


