Small large subgroups of a topological group
Abstract
This paper presents the following general structure theorem for topological groups.
Let G be a topological group of density 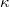 , for any cardinal
, for any cardinal 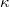 . Then each neighbourhood of the identity in G contains a subgroup of index less than or equal to
. Then each neighbourhood of the identity in G contains a subgroup of index less than or equal to 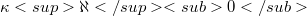 .
.
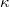 , for any cardinal
, for any cardinal 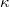 . Then each neighbourhood of the identity in G contains a subgroup of index less than or equal to
. Then each neighbourhood of the identity in G contains a subgroup of index less than or equal to 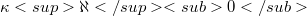 .
.DOI Code:
10.1285/i15900932v14n2p161
Full Text: PDF


