The existence of a straight line of piecewise Riemannian 2-manifolds

Abstract

In this paper, we study properties of piecewise Riemannian 2-maniflods which are combinatorial 2-manifolds such that each 2-simplex is a geodesic triangle of some Riemannian 2-manifolds. We will introduce the total excess 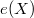of a piecewise Riemannian 2-manifold X and prove the following generalizations of results of Cohn-Vossen and the second author obtained for Riemannian 2-manifolds. Let X a piecewise Riemannian 2-manifolds without boundary having one end.