On homogeneous hypersurfaces in the manifold of quaternionic subalgebras of the Cayley algebra
Abstract
In this work we consider a class of real hypersurfaces of 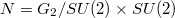 , the manifold of quaternionic subalgebras of the Cayley algebra. They are the family of tubes centered at the maximal totally geodesic submanifolds of maximal rank of
, the manifold of quaternionic subalgebras of the Cayley algebra. They are the family of tubes centered at the maximal totally geodesic submanifolds of maximal rank of 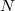 , which are (up to isomorphism)
, which are (up to isomorphism) 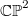 and
and 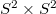 . We determine which of those tubes are homogeneous and for them we obtain the spectral decomposition of the shape operator. Moreover we show that the universal covering space of the focal set of
. We determine which of those tubes are homogeneous and for them we obtain the spectral decomposition of the shape operator. Moreover we show that the universal covering space of the focal set of 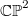 is the sphere
is the sphere 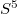 .
.
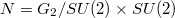 , the manifold of quaternionic subalgebras of the Cayley algebra. They are the family of tubes centered at the maximal totally geodesic submanifolds of maximal rank of
, the manifold of quaternionic subalgebras of the Cayley algebra. They are the family of tubes centered at the maximal totally geodesic submanifolds of maximal rank of 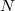 , which are (up to isomorphism)
, which are (up to isomorphism) 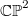 and
and 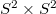 . We determine which of those tubes are homogeneous and for them we obtain the spectral decomposition of the shape operator. Moreover we show that the universal covering space of the focal set of
. We determine which of those tubes are homogeneous and for them we obtain the spectral decomposition of the shape operator. Moreover we show that the universal covering space of the focal set of 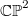 is the sphere
is the sphere 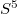 .
.DOI Code:
10.1285/i15900932v21n2p119
Keywords:
Manifold of quaternionic algebras; Hypersurfaces; Tubes; Shape operator; Jacobi operator
Classification:
53C30; 53C35; 53C42
Full Text: PDF


