New generalization of cubic partition of 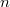
Abstract
Let 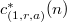 be the generalization of the cubic partition function
be the generalization of the cubic partition function 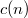 . In this paper, we prove some new congruences modulo odd prime
. In this paper, we prove some new congruences modulo odd prime 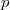 by taking
by taking 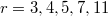 and
and 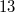 using
using 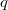 -series identities. We study congruence properties of generalization of cubic partition function for different values of
-series identities. We study congruence properties of generalization of cubic partition function for different values of  and give some particular cases as examples.
and give some particular cases as examples.
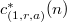 be the generalization of the cubic partition function
be the generalization of the cubic partition function 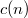 . In this paper, we prove some new congruences modulo odd prime
. In this paper, we prove some new congruences modulo odd prime 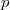 by taking
by taking 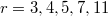 and
and 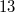 using
using 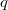 -series identities. We study congruence properties of generalization of cubic partition function for different values of
-series identities. We study congruence properties of generalization of cubic partition function for different values of  and give some particular cases as examples.
and give some particular cases as examples.DOI Code:
10.1285/i15900932v42n2p7
Keywords:
Partitions; k-colors; Partition Congruences
Full Text: PDF


