Bilateral Riemann-Liouville Fractional Sobolev spaces
Abstract
We establish some notation and properties of the bilateral Riemann-Liouville fractional derivative 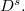 We introduce the associated Sobolev spaces of fractional order
We introduce the associated Sobolev spaces of fractional order  , denoted by
, denoted by 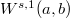 , and the Bounded Variation spaces of fractional order
, and the Bounded Variation spaces of fractional order  , denoted by
, denoted by 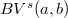 : these spaces are studied with the aim of providing a suitable functional framework for fractional variational models in image analysis.
: these spaces are studied with the aim of providing a suitable functional framework for fractional variational models in image analysis.
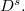 We introduce the associated Sobolev spaces of fractional order
We introduce the associated Sobolev spaces of fractional order  , denoted by
, denoted by 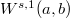 , and the Bounded Variation spaces of fractional order
, and the Bounded Variation spaces of fractional order  , denoted by
, denoted by 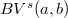 : these spaces are studied with the aim of providing a suitable functional framework for fractional variational models in image analysis.
: these spaces are studied with the aim of providing a suitable functional framework for fractional variational models in image analysis.DOI Code:
10.1285/i15900932v41n2p61
Keywords:
Fractional Calculus; Fractional Sobolev and BV Spaces
Full Text: PDF


