Open 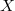 -ranks with respect to Segre and Veronese varieties
-ranks with respect to Segre and Veronese varieties
Abstract
Let 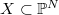 be an integral and non-degenerate variety. Recall (A. Bialynicki-Birula, A. Schinzel, J. Jelisiejew and others) that for any
be an integral and non-degenerate variety. Recall (A. Bialynicki-Birula, A. Schinzel, J. Jelisiejew and others) that for any 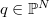 the open rank
the open rank 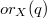 is the minimal positive integer such that for each closed set
is the minimal positive integer such that for each closed set 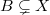 there is a set
there is a set 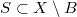 with
with 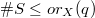 and
and 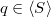 , where
, where 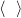 denotes the linear span. For an arbitrary
denotes the linear span. For an arbitrary 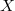 we give an upper bound for
we give an upper bound for 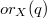 in terms of the upper bound for
in terms of the upper bound for 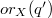 when
when 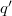 is a point in the maximal proper secant variety of
is a point in the maximal proper secant variety of 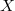 and a similar result using only points
and a similar result using only points 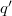 with submaximal border rank. We study
with submaximal border rank. We study 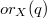 when
when 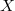 is a Segre variety (points with
is a Segre variety (points with 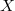 -rank
-rank 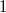 and
and 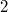 ) and when
) and when 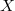 is a Veronese variety (points with
is a Veronese variety (points with 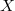 -rank
-rank 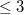 or with border rank
or with border rank 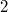 ).
).
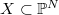 be an integral and non-degenerate variety. Recall (A. Bialynicki-Birula, A. Schinzel, J. Jelisiejew and others) that for any
be an integral and non-degenerate variety. Recall (A. Bialynicki-Birula, A. Schinzel, J. Jelisiejew and others) that for any 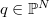 the open rank
the open rank 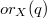 is the minimal positive integer such that for each closed set
is the minimal positive integer such that for each closed set 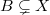 there is a set
there is a set 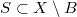 with
with 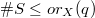 and
and 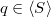 , where
, where 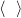 denotes the linear span. For an arbitrary
denotes the linear span. For an arbitrary 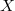 we give an upper bound for
we give an upper bound for 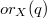 in terms of the upper bound for
in terms of the upper bound for 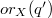 when
when 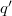 is a point in the maximal proper secant variety of
is a point in the maximal proper secant variety of 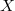 and a similar result using only points
and a similar result using only points 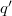 with submaximal border rank. We study
with submaximal border rank. We study 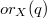 when
when 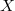 is a Segre variety (points with
is a Segre variety (points with 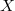 -rank
-rank 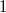 and
and 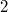 ) and when
) and when 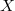 is a Veronese variety (points with
is a Veronese variety (points with 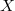 -rank
-rank 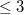 or with border rank
or with border rank 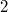 ).
).DOI Code:
10.1285/i15900932v41n1p19
Keywords:
open rank; open $X$-rank; Segre variety; Veronese variety; secant variety; border rank
Full Text: PDF


