On Defining the 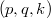 -Generalized Gamma Function
-Generalized Gamma Function
Abstract
In this paper, we introduce a 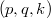 -generalization of the gamma function and investigate some basic identities and properties. Further, we define a
-generalization of the gamma function and investigate some basic identities and properties. Further, we define a 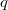 -integral representation for this function. As an application, we give some double inequalities concerning the
-integral representation for this function. As an application, we give some double inequalities concerning the 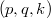 -generalized gamma function by using of its
-generalized gamma function by using of its 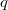 -integral representation.
-integral representation.
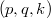 -generalization of the gamma function and investigate some basic identities and properties. Further, we define a
-generalization of the gamma function and investigate some basic identities and properties. Further, we define a 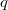 -integral representation for this function. As an application, we give some double inequalities concerning the
-integral representation for this function. As an application, we give some double inequalities concerning the 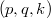 -generalized gamma function by using of its
-generalized gamma function by using of its 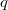 -integral representation.
-integral representation.DOI Code:
10.1285/i15900932v39n1p107
Keywords:
Gamma function; $q$-integral; $(p,q,k)$-generalized gamma function; $(p,q,k)$-generalized Pocchammer symbol; inequality
Full Text: PDF


