Alcune osservazioni su una classe di metodi lineari multistep A-stabili
Abstract
In this note we observe a decreasing property of 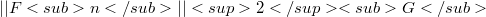 along the numerical solution of the autonomous differential system
along the numerical solution of the autonomous differential system 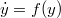 which satisfies a monotonicity condition; such a solution is obtained by means of a class of linear k-step A-stable methods and we have set(Error rendering LaTeX formula) and G is a symmetric positive definite matrix of order k.
We study also a particular subclass of linear multistep A-stable methods of maximum order, in which the matrix G is actually constructed.The associated Lyapunov function ensures the stability of the set of equilibrium points.
which satisfies a monotonicity condition; such a solution is obtained by means of a class of linear k-step A-stable methods and we have set(Error rendering LaTeX formula) and G is a symmetric positive definite matrix of order k.
We study also a particular subclass of linear multistep A-stable methods of maximum order, in which the matrix G is actually constructed.The associated Lyapunov function ensures the stability of the set of equilibrium points.
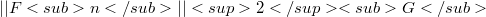 along the numerical solution of the autonomous differential system
along the numerical solution of the autonomous differential system 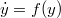 which satisfies a monotonicity condition; such a solution is obtained by means of a class of linear k-step A-stable methods and we have set(Error rendering LaTeX formula) and G is a symmetric positive definite matrix of order k.
We study also a particular subclass of linear multistep A-stable methods of maximum order, in which the matrix G is actually constructed.The associated Lyapunov function ensures the stability of the set of equilibrium points.
which satisfies a monotonicity condition; such a solution is obtained by means of a class of linear k-step A-stable methods and we have set(Error rendering LaTeX formula) and G is a symmetric positive definite matrix of order k.
We study also a particular subclass of linear multistep A-stable methods of maximum order, in which the matrix G is actually constructed.The associated Lyapunov function ensures the stability of the set of equilibrium points.DOI Code:
10.1285/i15900932v1n2p261
Full Text: PDF


