Sulle matrici torneo associate a matrici di permutazione
Abstract
A tournament matrix A is associated with a permutation matrix P if AP is still a tournament matrix.In this paper we consider the problem of the existence and the construction of such matrices and in particular we prove that A of order n is associated with a n-cycle P if and only if 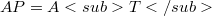 .In that case the tournament with A is rotational and the eigenvalues of A are determined.
.In that case the tournament with A is rotational and the eigenvalues of A are determined.
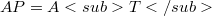 .In that case the tournament with A is rotational and the eigenvalues of A are determined.
.In that case the tournament with A is rotational and the eigenvalues of A are determined.DOI Code:
10.1285/i15900932v2n2p177
Full Text: PDF


