Designs embeddable in a plane cubic curve (Part 2 of Planar projective configurations)
Abstract
A configuration or a design K is a system of p points and m lines such that each point lies on 𝜋 of the lines and each line contains 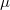 of the points.It is usually denoted by the symbol
of the points.It is usually denoted by the symbol 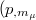 ,with
,with 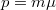 . A configuration
. A configuration 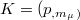 is said to have a geometric representation if we can draw it in the given geometry meaning that the points and lines of K correspond to points and lines in the geometry such that a point is incident with a line in K iff the same is true in the corresponding geometry. In this paper, we consider the problem of representing such combinatorial designs in the geometry of non-singular cubic curves over the complex projective plane. i. e. we study the problem of embedding them into a non-singular cubic curve in the complex projective plane in such a way that (ijk) is an element of the combinatorial design iff the points corresponding to
is said to have a geometric representation if we can draw it in the given geometry meaning that the points and lines of K correspond to points and lines in the geometry such that a point is incident with a line in K iff the same is true in the corresponding geometry. In this paper, we consider the problem of representing such combinatorial designs in the geometry of non-singular cubic curves over the complex projective plane. i. e. we study the problem of embedding them into a non-singular cubic curve in the complex projective plane in such a way that (ijk) is an element of the combinatorial design iff the points corresponding to 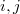 and k in the cubic curve are collinear.
and k in the cubic curve are collinear.
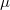 of the points.It is usually denoted by the symbol
of the points.It is usually denoted by the symbol 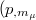 ,with
,with 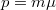 . A configuration
. A configuration 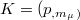 is said to have a geometric representation if we can draw it in the given geometry meaning that the points and lines of K correspond to points and lines in the geometry such that a point is incident with a line in K iff the same is true in the corresponding geometry. In this paper, we consider the problem of representing such combinatorial designs in the geometry of non-singular cubic curves over the complex projective plane. i. e. we study the problem of embedding them into a non-singular cubic curve in the complex projective plane in such a way that (ijk) is an element of the combinatorial design iff the points corresponding to
is said to have a geometric representation if we can draw it in the given geometry meaning that the points and lines of K correspond to points and lines in the geometry such that a point is incident with a line in K iff the same is true in the corresponding geometry. In this paper, we consider the problem of representing such combinatorial designs in the geometry of non-singular cubic curves over the complex projective plane. i. e. we study the problem of embedding them into a non-singular cubic curve in the complex projective plane in such a way that (ijk) is an element of the combinatorial design iff the points corresponding to 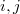 and k in the cubic curve are collinear.
and k in the cubic curve are collinear.DOI Code:
10.1285/i15900932v7n1p113
Full Text: PDF


