Postulation of general unions of lines and decorated lines
Abstract
A +line A 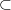
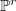 ,
, 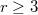 , is the scheme A = L
, is the scheme A = L 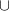
 with L a line and
with L a line and  a tangent vector of
a tangent vector of 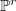 supported by a point of L, but not tangent to L. Here we prove that a general disjoint union of lines and +lines has the expected Hilbert function.
supported by a point of L, but not tangent to L. Here we prove that a general disjoint union of lines and +lines has the expected Hilbert function.
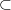
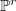 ,
, 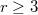 , is the scheme A = L
, is the scheme A = L 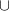
 with L a line and
with L a line and  a tangent vector of
a tangent vector of 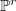 supported by a point of L, but not tangent to L. Here we prove that a general disjoint union of lines and +lines has the expected Hilbert function.
supported by a point of L, but not tangent to L. Here we prove that a general disjoint union of lines and +lines has the expected Hilbert function.DOI Code:
10.1285/i15900932v35n1p1
Keywords:
postulation; Hilbert function; lines; zero-dimensional schemes
Full Text: PDF


