Holomorphic functions on 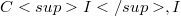 uncountable
uncountable
Abstract
In this article we show that 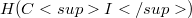 , the (Fréchet) holomorphic functions on
, the (Fréchet) holomorphic functions on 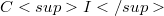 , is complete with respect to the topologies
, is complete with respect to the topologies 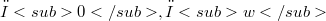 and
and 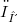 . The same result for countable I is well known (see [2]) since in this case
. The same result for countable I is well known (see [2]) since in this case 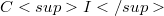 is a Fréchet space. The extension to uncountable I requires a different approach.For the compact open topology
is a Fréchet space. The extension to uncountable I requires a different approach.For the compact open topology 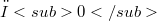 we use induction to reduce the problem to the countable case.Next we use the result for
we use induction to reduce the problem to the countable case.Next we use the result for 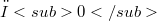 to reduce the problem for
to reduce the problem for 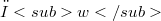 and
and 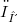 to the case of homogeneous polynomials.Using a method developed for holomorphic functions on nuclear Fréchet spaces with a basis and, once more,the result for the compact open topology we complete the proof for
to the case of homogeneous polynomials.Using a method developed for holomorphic functions on nuclear Fréchet spaces with a basis and, once more,the result for the compact open topology we complete the proof for 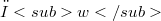 and
and 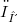 . We refer to [2] for background information.
. We refer to [2] for background information.
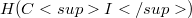 , the (Fréchet) holomorphic functions on
, the (Fréchet) holomorphic functions on 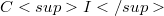 , is complete with respect to the topologies
, is complete with respect to the topologies 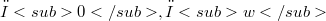 and
and 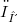 . The same result for countable I is well known (see [2]) since in this case
. The same result for countable I is well known (see [2]) since in this case 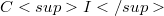 is a Fréchet space. The extension to uncountable I requires a different approach.For the compact open topology
is a Fréchet space. The extension to uncountable I requires a different approach.For the compact open topology 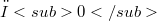 we use induction to reduce the problem to the countable case.Next we use the result for
we use induction to reduce the problem to the countable case.Next we use the result for 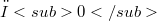 to reduce the problem for
to reduce the problem for 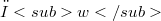 and
and 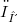 to the case of homogeneous polynomials.Using a method developed for holomorphic functions on nuclear Fréchet spaces with a basis and, once more,the result for the compact open topology we complete the proof for
to the case of homogeneous polynomials.Using a method developed for holomorphic functions on nuclear Fréchet spaces with a basis and, once more,the result for the compact open topology we complete the proof for 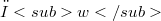 and
and 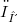 . We refer to [2] for background information.
. We refer to [2] for background information.DOI Code:
10.1285/i15900932v10supn1p65
Full Text: PDF


