Ideal properties and integral extension of convolution operators on 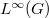
Abstract
We investigate operator ideal properties of convolution operators 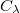 (via measures
(via measures 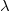 ) acting in
) acting in 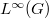 , with
, with  a compact abelian group. Of interest is when
a compact abelian group. Of interest is when 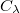 is compact, as this corresponds to
is compact, as this corresponds to 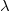 having an integrable density relative to Haar measure
having an integrable density relative to Haar measure 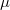 , i.e.,
, i.e., 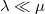 . Precisely then is there an \textit{optimal} Banach function space
. Precisely then is there an \textit{optimal} Banach function space 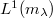 available which contains
available which contains 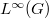 properly, densely and continuously and such that
properly, densely and continuously and such that 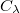 has a continuous,
has a continuous, 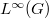 -valued, linear extension
-valued, linear extension 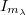 to
to 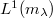 . A detailed study is made of
. A detailed study is made of 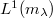 and
and 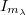 . Amongst other things, it is shown that
. Amongst other things, it is shown that 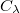 is compact iff the finitely additive,
is compact iff the finitely additive, 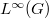 -valued set function
-valued set function 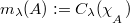 is norm
is norm 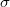 -additive iff
-additive iff 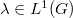 , whereas the corresponding optimal extension
, whereas the corresponding optimal extension 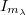 is compact iff
is compact iff 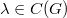 iff
iff 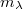 has finite variation. We also characterize when
has finite variation. We also characterize when 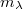 admits a Bochner (resp.\ Pettis)
admits a Bochner (resp.\ Pettis) 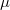 -integrable,
-integrable, 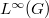 -valued density.
-valued density.
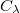 (via measures
(via measures 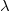 ) acting in
) acting in 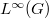 , with
, with  a compact abelian group. Of interest is when
a compact abelian group. Of interest is when 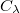 is compact, as this corresponds to
is compact, as this corresponds to 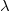 having an integrable density relative to Haar measure
having an integrable density relative to Haar measure 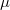 , i.e.,
, i.e., 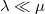 . Precisely then is there an \textit{optimal} Banach function space
. Precisely then is there an \textit{optimal} Banach function space 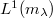 available which contains
available which contains 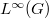 properly, densely and continuously and such that
properly, densely and continuously and such that 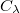 has a continuous,
has a continuous, 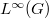 -valued, linear extension
-valued, linear extension 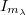 to
to 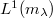 . A detailed study is made of
. A detailed study is made of 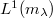 and
and 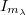 . Amongst other things, it is shown that
. Amongst other things, it is shown that 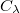 is compact iff the finitely additive,
is compact iff the finitely additive, 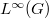 -valued set function
-valued set function 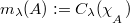 is norm
is norm 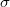 -additive iff
-additive iff 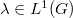 , whereas the corresponding optimal extension
, whereas the corresponding optimal extension 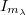 is compact iff
is compact iff 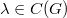 iff
iff 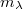 has finite variation. We also characterize when
has finite variation. We also characterize when 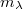 admits a Bochner (resp.\ Pettis)
admits a Bochner (resp.\ Pettis) 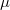 -integrable,
-integrable, 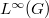 -valued density.
-valued density.DOI Code:
10.1285/i15900932v31n1p149
Keywords:
Convolution operator ; vector measure ; optimal domain ; Bochner-Pettis density
Full Text: PDF


