A characterization of groups of exponent 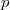 which are nilpotent of class at most 2
which are nilpotent of class at most 2
Abstract
Let 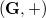 be a group of prime exponent
be a group of prime exponent 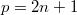 . In this paper we prove that
. In this paper we prove that 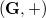 is nilpotent of class at most 2 if and only if one of the following properties is true:
is nilpotent of class at most 2 if and only if one of the following properties is true:
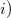
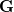 is also the support of a commutative group
is also the support of a commutative group 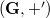 such that
such that 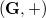 and
and 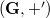 have the same cyclic cosets [cosets of order
have the same cyclic cosets [cosets of order 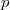 ].
]. 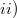 the operation
the operation 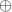 defined on
defined on 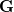 by putting
by putting 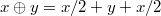 , gives
, gives 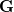 a structure of commutative group.\end
a structure of commutative group.\end
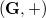 be a group of prime exponent
be a group of prime exponent 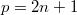 . In this paper we prove that
. In this paper we prove that 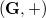 is nilpotent of class at most 2 if and only if one of the following properties is true:
is nilpotent of class at most 2 if and only if one of the following properties is true: 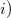
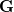 is also the support of a commutative group
is also the support of a commutative group 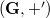 such that
such that 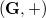 and
and 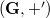 have the same cyclic cosets [cosets of order
have the same cyclic cosets [cosets of order 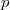 ].
]. 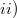 the operation
the operation 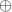 defined on
defined on 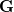 by putting
by putting 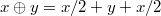 , gives
, gives 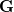 a structure of commutative group.\end
a structure of commutative group.\endDOI Code:
10.1285/i15900932v30n2p149
Keywords:
nilpotent groups; group partition
Full Text: PDF


