Symmetric spread sets
Abstract
Some new results on symplectic translation planes are given using their representation by spread sets of symmetric matrices. We provide a general construction of symplectic planes of even order and then consider the special case of planes of order 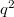 with kernel containing
with kernel containing 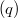 , stressing the role of Brown's theorem on ovoids containing a conic section. In particular we provide a criterion for a symplectic plane of even order
, stressing the role of Brown's theorem on ovoids containing a conic section. In particular we provide a criterion for a symplectic plane of even order 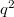 with kernel containing
with kernel containing 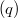 to be desarguesian. As a consequence we prove that a symplectic plane of even order
to be desarguesian. As a consequence we prove that a symplectic plane of even order 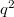 with kernel containing
with kernel containing 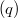 and admitting an affine homology of order
and admitting an affine homology of order 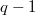 or a Baer involution fixing a totally isotropic
or a Baer involution fixing a totally isotropic 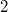 -subspace is desarguesian. Finally a short proof that symplectic semifield planes of even order
-subspace is desarguesian. Finally a short proof that symplectic semifield planes of even order 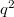 with kernel containing
with kernel containing 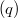 are desarguesian is given.
are desarguesian is given.
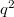 with kernel containing
with kernel containing 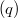 , stressing the role of Brown's theorem on ovoids containing a conic section. In particular we provide a criterion for a symplectic plane of even order
, stressing the role of Brown's theorem on ovoids containing a conic section. In particular we provide a criterion for a symplectic plane of even order 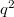 with kernel containing
with kernel containing 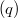 to be desarguesian. As a consequence we prove that a symplectic plane of even order
to be desarguesian. As a consequence we prove that a symplectic plane of even order 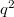 with kernel containing
with kernel containing 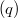 and admitting an affine homology of order
and admitting an affine homology of order 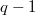 or a Baer involution fixing a totally isotropic
or a Baer involution fixing a totally isotropic 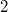 -subspace is desarguesian. Finally a short proof that symplectic semifield planes of even order
-subspace is desarguesian. Finally a short proof that symplectic semifield planes of even order 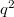 with kernel containing
with kernel containing 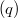 are desarguesian is given.
are desarguesian is given.DOI Code:
10.1285/i15900932v29n1supplp153
Keywords:
translation plane; symplectic spread; line-oval; affine homology; Baer involution
translation plane; symplectic spread; line-oval; affine homology; Baer involution
Full Text: PDF


