Symmetries which preserve the characteristic vector field of K-contact manifolds
Abstract
As is well-known locally symmetric K-contact manifolds are spaces of constant curvature ([13]).This means that having isometric local geodesic symmetries is a very strong restriction for K-contact manifolds.Thus other classes of isometries shall fit for contact geometry. For example, T. Takahashi [15] has introduced the notion of 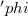 -geodesic symmetries on Sasaki manifolds and also on K-contact manifolds. Since then, manifolds with such isometries have been studied extensively.In this paper we generalize the notion of
-geodesic symmetries on Sasaki manifolds and also on K-contact manifolds. Since then, manifolds with such isometries have been studied extensively.In this paper we generalize the notion of 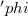 -geodesic symmetries. Because we notice that our diffeomorphisms preserve the characteristic vector field
-geodesic symmetries. Because we notice that our diffeomorphisms preserve the characteristic vector field 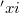 of K-contact manifolds, we call them symmetries which preserve the characteristic vector-field, or
of K-contact manifolds, we call them symmetries which preserve the characteristic vector-field, or 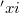 -preserving symmetries.Our idea for a construction of such local diffeomorphisms on K-contact manifolds is the lifting of symmetries on almost Kähler manifolds through the local fibering
-preserving symmetries.Our idea for a construction of such local diffeomorphisms on K-contact manifolds is the lifting of symmetries on almost Kähler manifolds through the local fibering 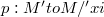 of K-contact manifolds.After recalling elementary facts on contact geometry in Section 1, we devote Section 2 to our definition of symmetries which preserve the characteristic vector field.Also we construct such a family of symmetries, which is an example of local S-rotations around curves in the sense of L. Nicolodi and L. Vanhecke [11].In Section 3 we give some examples of our symmetries.
of K-contact manifolds.After recalling elementary facts on contact geometry in Section 1, we devote Section 2 to our definition of symmetries which preserve the characteristic vector field.Also we construct such a family of symmetries, which is an example of local S-rotations around curves in the sense of L. Nicolodi and L. Vanhecke [11].In Section 3 we give some examples of our symmetries.
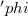 -geodesic symmetries on Sasaki manifolds and also on K-contact manifolds. Since then, manifolds with such isometries have been studied extensively.In this paper we generalize the notion of
-geodesic symmetries on Sasaki manifolds and also on K-contact manifolds. Since then, manifolds with such isometries have been studied extensively.In this paper we generalize the notion of 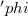 -geodesic symmetries. Because we notice that our diffeomorphisms preserve the characteristic vector field
-geodesic symmetries. Because we notice that our diffeomorphisms preserve the characteristic vector field 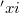 of K-contact manifolds, we call them symmetries which preserve the characteristic vector-field, or
of K-contact manifolds, we call them symmetries which preserve the characteristic vector-field, or 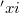 -preserving symmetries.Our idea for a construction of such local diffeomorphisms on K-contact manifolds is the lifting of symmetries on almost Kähler manifolds through the local fibering
-preserving symmetries.Our idea for a construction of such local diffeomorphisms on K-contact manifolds is the lifting of symmetries on almost Kähler manifolds through the local fibering 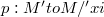 of K-contact manifolds.After recalling elementary facts on contact geometry in Section 1, we devote Section 2 to our definition of symmetries which preserve the characteristic vector field.Also we construct such a family of symmetries, which is an example of local S-rotations around curves in the sense of L. Nicolodi and L. Vanhecke [11].In Section 3 we give some examples of our symmetries.
of K-contact manifolds.After recalling elementary facts on contact geometry in Section 1, we devote Section 2 to our definition of symmetries which preserve the characteristic vector field.Also we construct such a family of symmetries, which is an example of local S-rotations around curves in the sense of L. Nicolodi and L. Vanhecke [11].In Section 3 we give some examples of our symmetries.DOI Code:
10.1285/i15900932v13n2p229
Full Text: PDF


