Introduzione
Abstract
En
The tangent and cotangent spaces of a bundle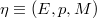 are considered, analysing their affine structure on the horizontal and the vertical spaces,respectively. When the bundle
are considered, analysing their affine structure on the horizontal and the vertical spaces,respectively. When the bundle 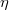 is affine or linear, further structures are considered. These results are specialised for
is affine or linear, further structures are considered. These results are specialised for 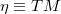 or
or 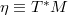 , finding interesting endomorphisms and isomorphisms. The Lie derivatives of tensors and the connections on bundle are introduced and analysed in strict relation with the affine structure of the tangent bundles.
, finding interesting endomorphisms and isomorphisms. The Lie derivatives of tensors and the connections on bundle are introduced and analysed in strict relation with the affine structure of the tangent bundles.
The tangent and cotangent spaces of a bundle
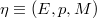 are considered, analysing their affine structure on the horizontal and the vertical spaces,respectively. When the bundle
are considered, analysing their affine structure on the horizontal and the vertical spaces,respectively. When the bundle 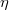 is affine or linear, further structures are considered. These results are specialised for
is affine or linear, further structures are considered. These results are specialised for 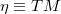 or
or 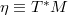 , finding interesting endomorphisms and isomorphisms. The Lie derivatives of tensors and the connections on bundle are introduced and analysed in strict relation with the affine structure of the tangent bundles.
, finding interesting endomorphisms and isomorphisms. The Lie derivatives of tensors and the connections on bundle are introduced and analysed in strict relation with the affine structure of the tangent bundles.DOI Code:
§
Full Text: PDF


