Countably enlarging weak barrelledness
Abstract
If 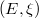 is a locally convex space with dual
is a locally convex space with dual 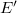 and
and 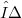 is the coarsest topology finer than
is the coarsest topology finer than 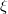 such that the dual of
such that the dual of 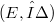 is
is 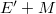 for a given
for a given 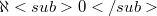 -dimensional subspace
-dimensional subspace 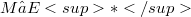 transverse to
transverse to 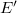 , then
, then 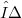 is a countable enlargement
is a countable enlargement 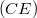 of
of 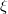 . Here most barrelled
. Here most barrelled 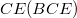 results are optimally extended within the fourteen properties introduced in the 1960s, '70s, '80s, '90s and recently studied in "Reinventing weak barrelledness", et al. If a
results are optimally extended within the fourteen properties introduced in the 1960s, '70s, '80s, '90s and recently studied in "Reinventing weak barrelledness", et al. If a 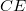 exists, one exists with none of the fourteen properties. Yet
exists, one exists with none of the fourteen properties. Yet 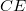 s that preserve precise subsets of these properties essentially double the stock of distinguishing examples. If a
s that preserve precise subsets of these properties essentially double the stock of distinguishing examples. If a 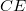 exists, must one exist that preserves a given property enjoyed by
exists, must one exist that preserves a given property enjoyed by 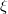 ? Under metrizability, the fourteen cases become two: the metrizable
? Under metrizability, the fourteen cases become two: the metrizable 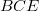 question we answered earlier, and the metrizable inductive
question we answered earlier, and the metrizable inductive 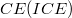 question we answer here (both positively). Without metrizability we are as yet unable to answer Robertson, Tweddle and Yeomans' original
question we answer here (both positively). Without metrizability we are as yet unable to answer Robertson, Tweddle and Yeomans' original 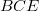 question (1979), the
question (1979), the 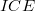 question and four others. We give negative answers for the eight remaining general cases, those between
question and four others. We give negative answers for the eight remaining general cases, those between 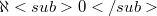 - barrelled and dual locally complete, inclusive, under the
- barrelled and dual locally complete, inclusive, under the 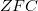 -consistent assumption
that
-consistent assumption
that 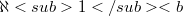 .
.
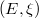 is a locally convex space with dual
is a locally convex space with dual 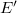 and
and 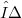 is the coarsest topology finer than
is the coarsest topology finer than 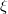 such that the dual of
such that the dual of 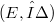 is
is 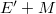 for a given
for a given 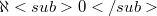 -dimensional subspace
-dimensional subspace 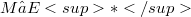 transverse to
transverse to 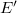 , then
, then 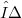 is a countable enlargement
is a countable enlargement 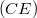 of
of 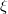 . Here most barrelled
. Here most barrelled 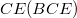 results are optimally extended within the fourteen properties introduced in the 1960s, '70s, '80s, '90s and recently studied in "Reinventing weak barrelledness", et al. If a
results are optimally extended within the fourteen properties introduced in the 1960s, '70s, '80s, '90s and recently studied in "Reinventing weak barrelledness", et al. If a 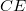 exists, one exists with none of the fourteen properties. Yet
exists, one exists with none of the fourteen properties. Yet 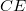 s that preserve precise subsets of these properties essentially double the stock of distinguishing examples. If a
s that preserve precise subsets of these properties essentially double the stock of distinguishing examples. If a 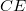 exists, must one exist that preserves a given property enjoyed by
exists, must one exist that preserves a given property enjoyed by 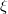 ? Under metrizability, the fourteen cases become two: the metrizable
? Under metrizability, the fourteen cases become two: the metrizable 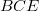 question we answered earlier, and the metrizable inductive
question we answered earlier, and the metrizable inductive 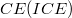 question we answer here (both positively). Without metrizability we are as yet unable to answer Robertson, Tweddle and Yeomans' original
question we answer here (both positively). Without metrizability we are as yet unable to answer Robertson, Tweddle and Yeomans' original 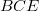 question (1979), the
question (1979), the 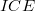 question and four others. We give negative answers for the eight remaining general cases, those between
question and four others. We give negative answers for the eight remaining general cases, those between 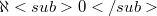 - barrelled and dual locally complete, inclusive, under the
- barrelled and dual locally complete, inclusive, under the 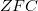 -consistent assumption
that
-consistent assumption
that 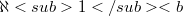 .
.DOI Code:
10.1285/i15900932v17p217
Full Text: PDF


