Diagonal operators, s-numbers and Bernstein pairs
Abstract
Replacing the nested sequence of "finite" dimensional subspaces by the nested sequence of "closed" subspaces in the classical Bernstein lethargy theorem, we obtain a version of this theorem for the space 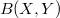 of all bounded linear maps. Using this result and some properties of diagonal operators, we investigate conditions under which a suitable pair of Banach spaces form an exact Bernstein pair. We also show that many "classical" Banach spaces, including the couple
of all bounded linear maps. Using this result and some properties of diagonal operators, we investigate conditions under which a suitable pair of Banach spaces form an exact Bernstein pair. We also show that many "classical" Banach spaces, including the couple ![(L<sub>p</sub>[0,1], L<sub>q</sub>[0,1])](http://212.189.136.205/plugins/generic/latexRender/cache/39aebaa7f1923c4bf4bd64a1efea4f71.png) form a Bernstein pair with respect to any sequence of s- numbers
form a Bernstein pair with respect to any sequence of s- numbers 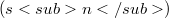 , for
, for 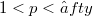 and
and 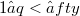 .
.
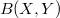 of all bounded linear maps. Using this result and some properties of diagonal operators, we investigate conditions under which a suitable pair of Banach spaces form an exact Bernstein pair. We also show that many "classical" Banach spaces, including the couple
of all bounded linear maps. Using this result and some properties of diagonal operators, we investigate conditions under which a suitable pair of Banach spaces form an exact Bernstein pair. We also show that many "classical" Banach spaces, including the couple ![(L<sub>p</sub>[0,1], L<sub>q</sub>[0,1])](http://212.189.136.205/plugins/generic/latexRender/cache/39aebaa7f1923c4bf4bd64a1efea4f71.png) form a Bernstein pair with respect to any sequence of s- numbers
form a Bernstein pair with respect to any sequence of s- numbers 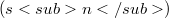 , for
, for 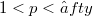 and
and 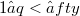 .
.DOI Code:
10.1285/i15900932v17p209
Full Text: PDF


