Hankel operators on generalized Bergman-Hardy spaces
Abstract
We study Hankel operators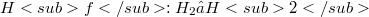 
on a class of spaces 
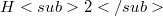of analytic functions which includes, among many other examples, the Hardy space and the Bergman spaces obn the unit disk as well as the Fock space on 
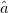. We derive compactness conditions for 
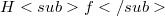and describe the essential spectrum of 
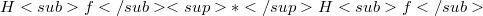. Moreover we investigate Schatten class Hankel operators. The main objects of study are those Hankel operators 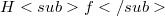which admit a sequence of vector-valued trigonometric polynomials 
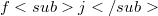with(Error rendering LaTeX formula).
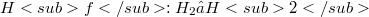on a class of spaces 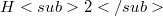of analytic functions which includes, among many other examples, the Hardy space and the Bergman spaces obn the unit disk as well as the Fock space on 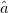. We derive compactness conditions for 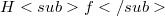and describe the essential spectrum of 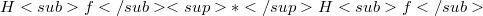. Moreover we investigate Schatten class Hankel operators. The main objects of study are those Hankel operators 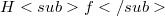which admit a sequence of vector-valued trigonometric polynomials 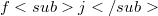with(Error rendering LaTeX formula).DOI Code:
10.1285/i15900932v17p71
Keywords:
Hankel operators; Toeplitz operators; Bergman-Hardy spaces; Compact operators; Schatten class operators; Fourier series
Classification:
47B35; 47B38; 46E20; 42B05
Full Text: PDF
