On a class of rational matrices and interpolating polynomials related to the discrete Laplace operator
Abstract
Let  be the discrete Laplace operator acting on functions(or rational matrices)
be the discrete Laplace operator acting on functions(or rational matrices) 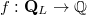 ,where
,where 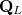 is the two dimensional lattice of size
is the two dimensional lattice of size 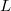 embedded in
embedded in 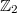 . Consider a rational
. Consider a rational 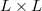 matrix
matrix 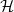 , whose inner entries
, whose inner entries 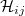 satisfy
satisfy 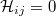 . The matrix
. The matrix 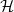 is thus theclassical finite difference five-points approximation of theLaplace operator in two variables. We give a constructive proofthat
is thus theclassical finite difference five-points approximation of theLaplace operator in two variables. We give a constructive proofthat 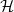 is the restriction to
is the restriction to 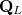 of adiscrete harmonic polynomial in two variables for any
of adiscrete harmonic polynomial in two variables for any 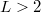 . Thisresult proves a conjecture formulated in the context ofdeterministic fixed-energy sandpile models in statisticalmechanics.
. Thisresult proves a conjecture formulated in the context ofdeterministic fixed-energy sandpile models in statisticalmechanics.
 be the discrete Laplace operator acting on functions(or rational matrices)
be the discrete Laplace operator acting on functions(or rational matrices) 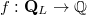 ,where
,where 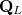 is the two dimensional lattice of size
is the two dimensional lattice of size 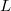 embedded in
embedded in 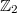 . Consider a rational
. Consider a rational 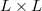 matrix
matrix 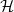 , whose inner entries
, whose inner entries 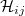 satisfy
satisfy 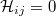 . The matrix
. The matrix 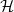 is thus theclassical finite difference five-points approximation of theLaplace operator in two variables. We give a constructive proofthat
is thus theclassical finite difference five-points approximation of theLaplace operator in two variables. We give a constructive proofthat 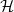 is the restriction to
is the restriction to 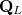 of adiscrete harmonic polynomial in two variables for any
of adiscrete harmonic polynomial in two variables for any 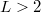 . Thisresult proves a conjecture formulated in the context ofdeterministic fixed-energy sandpile models in statisticalmechanics.
. Thisresult proves a conjecture formulated in the context ofdeterministic fixed-energy sandpile models in statisticalmechanics.DOI Code:
10.1285/i15900932v28n2p1
Keywords:
rational matrices; discrete Laplacian; discrete harmonic polynomials; sandpile
Classification:
11C99 (Polynomials and matrices)
Full Text: PDF


