Analysis of the harmonic flow of geometric structures
Abstract
We develop an analysis of the flow of harmonic 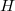 -structures with the strategy introduced by Chen-Struwe for the harmonic map heat equation when the target does not necessarily have negative sectional curvature, so the Eells-Sampson Theorem cannot apply. In particular, this flow method enables us to find theoretical hypotheses under which the existence of a torsion-free
-structures with the strategy introduced by Chen-Struwe for the harmonic map heat equation when the target does not necessarily have negative sectional curvature, so the Eells-Sampson Theorem cannot apply. In particular, this flow method enables us to find theoretical hypotheses under which the existence of a torsion-free 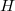 -structure is guaranteed and conditions for which the flow must blow up in finite time. This extends results already known for some specific groups like
-structure is guaranteed and conditions for which the flow must blow up in finite time. This extends results already known for some specific groups like 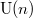 ,
, 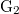 or
or 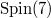 .
.
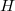 -structures with the strategy introduced by Chen-Struwe for the harmonic map heat equation when the target does not necessarily have negative sectional curvature, so the Eells-Sampson Theorem cannot apply. In particular, this flow method enables us to find theoretical hypotheses under which the existence of a torsion-free
-structures with the strategy introduced by Chen-Struwe for the harmonic map heat equation when the target does not necessarily have negative sectional curvature, so the Eells-Sampson Theorem cannot apply. In particular, this flow method enables us to find theoretical hypotheses under which the existence of a torsion-free 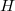 -structure is guaranteed and conditions for which the flow must blow up in finite time. This extends results already known for some specific groups like
-structure is guaranteed and conditions for which the flow must blow up in finite time. This extends results already known for some specific groups like 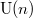 ,
, 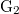 or
or 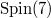 .
.DOI Code:
10.1285/i15900932v45s1p129
Keywords:
Geometric structures; harmonic maps; harmonic sections; heat flow
Full Text: PDF


