On some Lusternick-Schnirelmann type invariants
Abstract
In this paper, we show that the invariant  , introduced in [15], coincides with
, introduced in [15], coincides with 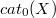 for any rationally elliptic space
for any rationally elliptic space 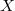 . Additionally, we define, for any space
. Additionally, we define, for any space 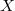 over an arbitrary field
over an arbitrary field  , an
, an 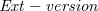 homotpy invariant
homotpy invariant 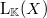 of the Ginsburg invariant
of the Ginsburg invariant 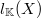 . Then, we establish the equality between
. Then, we establish the equality between 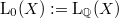 and
and 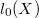 in the case where
in the case where 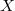 is rationally elliptic.
is rationally elliptic.
 , introduced in [15], coincides with
, introduced in [15], coincides with 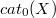 for any rationally elliptic space
for any rationally elliptic space 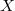 . Additionally, we define, for any space
. Additionally, we define, for any space 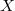 over an arbitrary field
over an arbitrary field  , an
, an 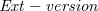 homotpy invariant
homotpy invariant 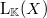 of the Ginsburg invariant
of the Ginsburg invariant 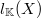 . Then, we establish the equality between
. Then, we establish the equality between 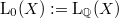 and
and 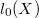 in the case where
in the case where 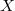 is rationally elliptic.
is rationally elliptic.DOI Code:
10.1285/i15900932v45s1p1
Keywords:
LS-category; Toomer and Ginsburg invariants; Milnor-Moore and Eilenberg-Moore spectral sequences
Full Text: PDF


