An isomorphism between projective models of toric and hyperplane graphic arrangements
Abstract
This paper presents a bridge between the theories of wonderful models associated with toric arrangements and wonderful models associated with hyperplane arrangements. In a previous work, the same authors noticed that the model of the toric arrangement of type 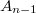 associated with the minimal building set is isomorphic to the one of the hyperplane arrangement of type
associated with the minimal building set is isomorphic to the one of the hyperplane arrangement of type 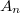 associated again with the minimal building set; it is natural to ask if there exist similar isomorphisms between other families of arrangements. The aim of this paper is to study one such family, namely the family of arrangements defined by graphs. The main result states that there is indeed an isomorphism between the model of the toric arrangement defined by a graph
associated again with the minimal building set; it is natural to ask if there exist similar isomorphisms between other families of arrangements. The aim of this paper is to study one such family, namely the family of arrangements defined by graphs. The main result states that there is indeed an isomorphism between the model of the toric arrangement defined by a graph 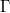 and the model of the hyperplane arrangement defined by the cone of
and the model of the hyperplane arrangement defined by the cone of 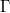 , provided that a suitable building set is chosen.
, provided that a suitable building set is chosen.
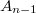 associated with the minimal building set is isomorphic to the one of the hyperplane arrangement of type
associated with the minimal building set is isomorphic to the one of the hyperplane arrangement of type 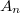 associated again with the minimal building set; it is natural to ask if there exist similar isomorphisms between other families of arrangements. The aim of this paper is to study one such family, namely the family of arrangements defined by graphs. The main result states that there is indeed an isomorphism between the model of the toric arrangement defined by a graph
associated again with the minimal building set; it is natural to ask if there exist similar isomorphisms between other families of arrangements. The aim of this paper is to study one such family, namely the family of arrangements defined by graphs. The main result states that there is indeed an isomorphism between the model of the toric arrangement defined by a graph 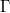 and the model of the hyperplane arrangement defined by the cone of
and the model of the hyperplane arrangement defined by the cone of 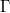 , provided that a suitable building set is chosen.
, provided that a suitable building set is chosen.DOI Code:
10.1285/i15900932v45n1p15
Keywords:
Toric arrangements; Compact models; Configuration spaces
Full Text: PDF


