Uniform Sobolev, interpolation and geometric Calderón-Zygmund inequalities for graph hypersurfaces
Abstract
In this note, our aim is to show that families of smooth hypersurfaces of 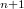 which are all "
which are all "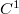 -close" enough to a fixed compact, embedded one, have uniformly bounded constants in some relevant inequalities for mathematical analysis, like Sobolev, Gagliardo-Nirenberg and "geometric" Calderón-Zygmund inequalities.
-close" enough to a fixed compact, embedded one, have uniformly bounded constants in some relevant inequalities for mathematical analysis, like Sobolev, Gagliardo-Nirenberg and "geometric" Calderón-Zygmund inequalities.
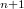 which are all "
which are all "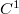 -close" enough to a fixed compact, embedded one, have uniformly bounded constants in some relevant inequalities for mathematical analysis, like Sobolev, Gagliardo-Nirenberg and "geometric" Calderón-Zygmund inequalities.
-close" enough to a fixed compact, embedded one, have uniformly bounded constants in some relevant inequalities for mathematical analysis, like Sobolev, Gagliardo-Nirenberg and "geometric" Calderón-Zygmund inequalities.DOI Code:
10.1285/i15900932v44n1p53
Keywords:
Embedded hypersurface; Sobolev inequalities; interpolation inequalities; Calderón-Zygmund inequalities
Full Text: PDF


