Genus One Almost Simple Groups of Lie Rank Two
Abstract
In this paper, we assume that  is a finite group with socle
is a finite group with socle 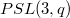 and
and  acts on the projective points of 2-dimensional projective geometry
acts on the projective points of 2-dimensional projective geometry 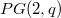 ,
, 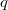 is a prime power. By using a new method, we show that
is a prime power. By using a new method, we show that  possesses no genus one group if
possesses no genus one group if 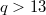 . Furthermore, we study the connectedness of the Hurwitz space
. Furthermore, we study the connectedness of the Hurwitz space 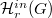 for a given group
for a given group  , genus one and
, genus one and 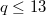 .
.
 is a finite group with socle
is a finite group with socle 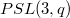 and
and  acts on the projective points of 2-dimensional projective geometry
acts on the projective points of 2-dimensional projective geometry 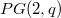 ,
, 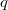 is a prime power. By using a new method, we show that
is a prime power. By using a new method, we show that  possesses no genus one group if
possesses no genus one group if 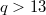 . Furthermore, we study the connectedness of the Hurwitz space
. Furthermore, we study the connectedness of the Hurwitz space 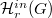 for a given group
for a given group  , genus one and
, genus one and 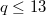 .
.DOI Code:
10.1285/i15900932v43n2p67
Keywords:
Projective special linear group; Fixed point ratio; Genus one group
Full Text: PDF


