Quantum Operations in Algebraic QFT
Abstract
Conformal Quantum Field Theories (CFT) in 1 or 1+1 spacetime dimensions (respectively called chiral and full CFTs) admit several "axiomatic" (mathematically rigorous and model-independent) formulations. In this note, we deal with the von Neumann algebraic formulation due to Haag and Kastler [43], mainly restricted to the chiral CFT setting [18]. Irrespectively of the chosen formulation, one can ask the question s: given a theory 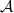 , how many and which are the possible extensions
, how many and which are the possible extensions 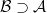 or subtheories
or subtheories 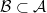 ? How to construct and classify them, and study their properties? Extensions are typically described in the language of
? How to construct and classify them, and study their properties? Extensions are typically described in the language of 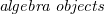 in the braided tensor category of representations of
in the braided tensor category of representations of 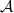 , while subtheories require different ideas. In this paper, we review recent structural results on the study of subtheories in the von Neumann algebraic formulation (conformal subnets) of a given chiral CFT (conformal net), [4], [5], [6], [7]. Furthermore, building on [7], we provide a "quantum Galois theory" for conformal nets analogous to the one for Vertex Operator Algebras (VOA) [28], [29]. We also outline the case of 3+1 dimensional Algebraic Quantum Field Theories (AQFT). The aforementioned results make use of families of (extreme) vacuum state preserving unital completely positive maps acting on the net of von Neumann algebras, hereafter called
, while subtheories require different ideas. In this paper, we review recent structural results on the study of subtheories in the von Neumann algebraic formulation (conformal subnets) of a given chiral CFT (conformal net), [4], [5], [6], [7]. Furthermore, building on [7], we provide a "quantum Galois theory" for conformal nets analogous to the one for Vertex Operator Algebras (VOA) [28], [29]. We also outline the case of 3+1 dimensional Algebraic Quantum Field Theories (AQFT). The aforementioned results make use of families of (extreme) vacuum state preserving unital completely positive maps acting on the net of von Neumann algebras, hereafter called 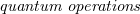 . These are natural generalizations of the ordinary vacuum preserving gauge automorphisms, hence they play the role of "generalized global gauge symmetries". Quantum operations suffice to describe
. These are natural generalizations of the ordinary vacuum preserving gauge automorphisms, hence they play the role of "generalized global gauge symmetries". Quantum operations suffice to describe 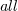 possible conformal subnets of a given conformal net with the same central charge.
possible conformal subnets of a given conformal net with the same central charge.
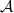 , how many and which are the possible extensions
, how many and which are the possible extensions 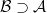 or subtheories
or subtheories 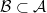 ? How to construct and classify them, and study their properties? Extensions are typically described in the language of
? How to construct and classify them, and study their properties? Extensions are typically described in the language of 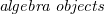 in the braided tensor category of representations of
in the braided tensor category of representations of 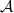 , while subtheories require different ideas. In this paper, we review recent structural results on the study of subtheories in the von Neumann algebraic formulation (conformal subnets) of a given chiral CFT (conformal net), [4], [5], [6], [7]. Furthermore, building on [7], we provide a "quantum Galois theory" for conformal nets analogous to the one for Vertex Operator Algebras (VOA) [28], [29]. We also outline the case of 3+1 dimensional Algebraic Quantum Field Theories (AQFT). The aforementioned results make use of families of (extreme) vacuum state preserving unital completely positive maps acting on the net of von Neumann algebras, hereafter called
, while subtheories require different ideas. In this paper, we review recent structural results on the study of subtheories in the von Neumann algebraic formulation (conformal subnets) of a given chiral CFT (conformal net), [4], [5], [6], [7]. Furthermore, building on [7], we provide a "quantum Galois theory" for conformal nets analogous to the one for Vertex Operator Algebras (VOA) [28], [29]. We also outline the case of 3+1 dimensional Algebraic Quantum Field Theories (AQFT). The aforementioned results make use of families of (extreme) vacuum state preserving unital completely positive maps acting on the net of von Neumann algebras, hereafter called 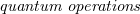 . These are natural generalizations of the ordinary vacuum preserving gauge automorphisms, hence they play the role of "generalized global gauge symmetries". Quantum operations suffice to describe
. These are natural generalizations of the ordinary vacuum preserving gauge automorphisms, hence they play the role of "generalized global gauge symmetries". Quantum operations suffice to describe 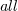 possible conformal subnets of a given conformal net with the same central charge.
possible conformal subnets of a given conformal net with the same central charge.DOI Code:
10.1285/i15900932v43n1p41
Keywords:
Conformal subnet; algebraic quantum field theory; quantum operation; unital completely positive map; hypergroup
Full Text: PDF


