On the Radio 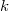 -chromatic Number of Paths
-chromatic Number of Paths
Abstract
A radio 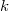 -coloring of a graph
-coloring of a graph  is an assignment
is an assignment 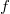 of positive integers (colors) to the vertices of
of positive integers (colors) to the vertices of  such that for any two vertices
such that for any two vertices 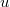 and
and  of
of  , the difference between their colors is at least
, the difference between their colors is at least 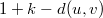 . The span
. The span 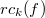 of
of 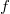 is
is 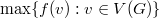 . The radio
. The radio 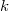 -chromatic number
-chromatic number 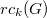 of
of  is
is 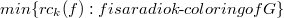 . In this paper, in an attempt to prove a conjecture on the radio
. In this paper, in an attempt to prove a conjecture on the radio 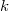 -chromatic number of path, we determine the radio
-chromatic number of path, we determine the radio 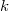 -chromatic number of paths
-chromatic number of paths 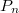 for
for 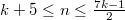 if
if 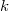 is odd and
is odd and 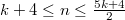 if
if 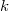 is even.
is even.
 -coloring of a graph
-coloring of a graph  is an assignment
is an assignment 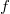 of positive integers (colors) to the vertices of
of positive integers (colors) to the vertices of  such that for any two vertices
such that for any two vertices 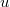 and
and  of
of  , the difference between their colors is at least
, the difference between their colors is at least 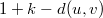 . The span
. The span 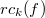 of
of 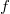 is
is 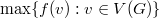 . The radio
. The radio 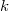 -chromatic number
-chromatic number 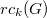 of
of  is
is 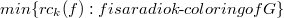 . In this paper, in an attempt to prove a conjecture on the radio
. In this paper, in an attempt to prove a conjecture on the radio 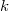 -chromatic number of path, we determine the radio
-chromatic number of path, we determine the radio 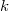 -chromatic number of paths
-chromatic number of paths 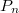 for
for 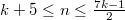 if
if 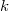 is odd and
is odd and 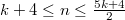 if
if 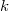 is even.
is even.DOI Code:
10.1285/i15900932v42n1p37
Keywords:
radio k-coloring; radio k-chromatic number; radio coloring; radio number
Full Text: PDF


