Some properties of the mapping 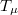 introduced by a representation in Banach and locally convex spaces
introduced by a representation in Banach and locally convex spaces
Abstract
Let 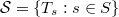 be a representation of a semigroup
be a representation of a semigroup 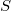 . We show that the mapping
. We show that the mapping 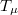 introduced by a mean on a subspace of
introduced by a mean on a subspace of 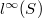 inherits some properties of
inherits some properties of 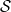 in Banach spaces and locally convex spaces. The notions of
in Banach spaces and locally convex spaces. The notions of 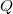 -
- -nonexpansive mapping and
-nonexpansive mapping and 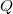 -
- -attractive point in locally convex spaces are introduced. We prove that
-attractive point in locally convex spaces are introduced. We prove that 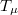 is a
is a 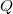 -
- -nonexpansive mapping when
-nonexpansive mapping when 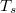 is
is 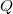 -
- -nonexpansive mapping for each
-nonexpansive mapping for each 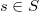 and a point in a locally convex space is
and a point in a locally convex space is 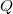 -
- -attractive point of
-attractive point of 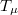 if it is a
if it is a 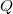 -
- -attractive point of
-attractive point of 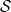 .
.
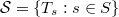 be a representation of a semigroup
be a representation of a semigroup 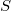 . We show that the mapping
. We show that the mapping 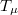 introduced by a mean on a subspace of
introduced by a mean on a subspace of 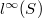 inherits some properties of
inherits some properties of 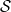 in Banach spaces and locally convex spaces. The notions of
in Banach spaces and locally convex spaces. The notions of 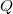 -
- -nonexpansive mapping and
-nonexpansive mapping and 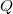 -
- -attractive point in locally convex spaces are introduced. We prove that
-attractive point in locally convex spaces are introduced. We prove that 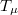 is a
is a 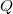 -
- -nonexpansive mapping when
-nonexpansive mapping when 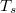 is
is 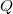 -
- -nonexpansive mapping for each
-nonexpansive mapping for each 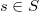 and a point in a locally convex space is
and a point in a locally convex space is 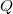 -
- -attractive point of
-attractive point of 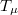 if it is a
if it is a 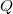 -
- -attractive point of
-attractive point of 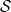 .
.DOI Code:
10.1285/i15900932v40n1p101
Keywords:
Representation; Nonexpansive; Attractive point; Directed graph; Mean
Full Text: PDF


