Hall Graph of a Finite Group
Abstract
The Hall graph of a finite group  is a simple graph whose vertex set is
is a simple graph whose vertex set is 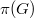 , the set of all prime divisors of its order, and two distinct primes
, the set of all prime divisors of its order, and two distinct primes 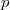 and
and 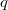 are joined by an edge if
are joined by an edge if  has at least one Hall
has at least one Hall 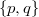 -subgroup. For all primes
-subgroup. For all primes 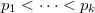 of
of 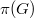 , we call the
, we call the 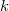 -tuple
-tuple 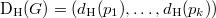 , the degree pattern of Hall graph of
, the degree pattern of Hall graph of  , where
, where 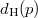 signifies the degree of vertex
signifies the degree of vertex 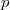 . This paper provides some properties of Hall graph. It also gives a characterization for some finite simple groups via order and degree pattern of Hall graph.
. This paper provides some properties of Hall graph. It also gives a characterization for some finite simple groups via order and degree pattern of Hall graph.
 is a simple graph whose vertex set is
is a simple graph whose vertex set is 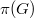 , the set of all prime divisors of its order, and two distinct primes
, the set of all prime divisors of its order, and two distinct primes 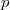 and
and 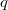 are joined by an edge if
are joined by an edge if  has at least one Hall
has at least one Hall 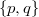 -subgroup. For all primes
-subgroup. For all primes 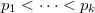 of
of 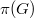 , we call the
, we call the 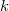 -tuple
-tuple 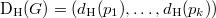 , the degree pattern of Hall graph of
, the degree pattern of Hall graph of  , where
, where 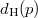 signifies the degree of vertex
signifies the degree of vertex 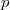 . This paper provides some properties of Hall graph. It also gives a characterization for some finite simple groups via order and degree pattern of Hall graph.
. This paper provides some properties of Hall graph. It also gives a characterization for some finite simple groups via order and degree pattern of Hall graph.DOI Code:
10.1285/i15900932v39n2p25
Keywords:
Hall graph; degree pattern of Hall graph; Hall subgroup; simple group
Full Text: PDF


