Existence and multiplicity results for Dirichlet boundary value problems involving the 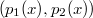 - Laplace operator
- Laplace operator
Abstract
This paper is concerned with the existence and multiplicity of solutions for the following Dirichlet boundary value problems involving the 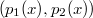 -Laplace operator of the form: \begin{equation*} \begin{gathered} -\operatorname{div}(|\nabla u|^{p_{1}(x)-2}\nabla u)- \operatorname{div}(|\nabla u|^{p_{2}(x)-2}\nabla u)= f(x,u) \quad\text{in } \Omega,\\ u=0 \quad \text{on } \partial\Omega. \end{gathered} \end{equation*} By means of critical point theorems with Cerami condition and the theory of the variable exponent Sobolev spaces, we establish the existence and multiplicity of solutions.
-Laplace operator of the form: \begin{equation*} \begin{gathered} -\operatorname{div}(|\nabla u|^{p_{1}(x)-2}\nabla u)- \operatorname{div}(|\nabla u|^{p_{2}(x)-2}\nabla u)= f(x,u) \quad\text{in } \Omega,\\ u=0 \quad \text{on } \partial\Omega. \end{gathered} \end{equation*} By means of critical point theorems with Cerami condition and the theory of the variable exponent Sobolev spaces, we establish the existence and multiplicity of solutions.
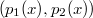 -Laplace operator of the form: \begin{equation*} \begin{gathered} -\operatorname{div}(|\nabla u|^{p_{1}(x)-2}\nabla u)- \operatorname{div}(|\nabla u|^{p_{2}(x)-2}\nabla u)= f(x,u) \quad\text{in } \Omega,\\ u=0 \quad \text{on } \partial\Omega. \end{gathered} \end{equation*} By means of critical point theorems with Cerami condition and the theory of the variable exponent Sobolev spaces, we establish the existence and multiplicity of solutions.
-Laplace operator of the form: \begin{equation*} \begin{gathered} -\operatorname{div}(|\nabla u|^{p_{1}(x)-2}\nabla u)- \operatorname{div}(|\nabla u|^{p_{2}(x)-2}\nabla u)= f(x,u) \quad\text{in } \Omega,\\ u=0 \quad \text{on } \partial\Omega. \end{gathered} \end{equation*} By means of critical point theorems with Cerami condition and the theory of the variable exponent Sobolev spaces, we establish the existence and multiplicity of solutions.DOI Code:
10.1285/i15900932v37n1p69
Keywords:
variational methods; generalized Lebesgue-Sobolev spaces
Full Text: PDF


