Holonomic spaces
Abstract
The purpose of this note is to give a synthetic description of the intrinsic metric of a fiber F of the connection metric on a vector bundle E 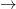 M over a riemannian manifold M endowed with a euclidean metric and a compatible connection. These metrics are described in terms of the action of the holonomy group and several properties are derived thereafter. In the process, a strong metric geometric meaning is given to the holonomy group.
M over a riemannian manifold M endowed with a euclidean metric and a compatible connection. These metrics are described in terms of the action of the holonomy group and several properties are derived thereafter. In the process, a strong metric geometric meaning is given to the holonomy group.
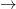 M over a riemannian manifold M endowed with a euclidean metric and a compatible connection. These metrics are described in terms of the action of the holonomy group and several properties are derived thereafter. In the process, a strong metric geometric meaning is given to the holonomy group.
M over a riemannian manifold M endowed with a euclidean metric and a compatible connection. These metrics are described in terms of the action of the holonomy group and several properties are derived thereafter. In the process, a strong metric geometric meaning is given to the holonomy group.DOI Code:
10.1285/i15900932v37suppl1p141
Keywords:
Holonomy; vector bundles; connection metrics; isoholonomic; geodesics
Full Text: PDF


