On some arithmetic properties of nite groups
Abstract
Let 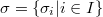 be some partition of the set of all primes
be some partition of the set of all primes 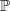 . A group
. A group 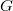 is called \emph{
is called \emph{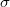 -primary} if
-primary} if 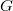 is a finite
is a finite 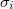 -group for some
-group for some 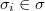 . We say that a finite group
. We say that a finite group 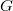 is: \emph{
is: \emph{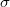 -soluble} if every chief factor of
-soluble} if every chief factor of 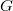 is
is 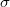 -primary; \emph{
-primary; \emph{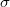 -nilpotent} if
-nilpotent} if 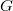 is the direct product of some
is the direct product of some 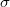 -primary groupsBeing based on these concepts, we develop and unify some aspects of the theories of soluble, nilpotent, supersoluble and quasinilpotent groups, the subgroup lattices theory, the theories of generalized quasinormal and generalized subnormal subgroups
-primary groupsBeing based on these concepts, we develop and unify some aspects of the theories of soluble, nilpotent, supersoluble and quasinilpotent groups, the subgroup lattices theory, the theories of generalized quasinormal and generalized subnormal subgroups
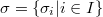 be some partition of the set of all primes
be some partition of the set of all primes 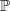 . A group
. A group 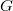 is called \emph{
is called \emph{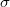 -primary} if
-primary} if 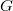 is a finite
is a finite 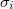 -group for some
-group for some 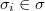 . We say that a finite group
. We say that a finite group 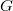 is: \emph{
is: \emph{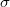 -soluble} if every chief factor of
-soluble} if every chief factor of 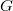 is
is 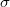 -primary; \emph{
-primary; \emph{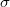 -nilpotent} if
-nilpotent} if 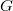 is the direct product of some
is the direct product of some 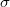 -primary groupsBeing based on these concepts, we develop and unify some aspects of the theories of soluble, nilpotent, supersoluble and quasinilpotent groups, the subgroup lattices theory, the theories of generalized quasinormal and generalized subnormal subgroups
-primary groupsBeing based on these concepts, we develop and unify some aspects of the theories of soluble, nilpotent, supersoluble and quasinilpotent groups, the subgroup lattices theory, the theories of generalized quasinormal and generalized subnormal subgroupsDOI Code:
10.1285/i15900932v36suppl1p65
Keywords:
finite group; Hall subgroup; $\Pi $-full group; $\Pi$-subnormal subgroup; $\sigma $-soluble group; $\sigma$-nilpotent subgroup
Full Text: PDF


