Planar projective configurations (Part 1)
Abstract
The problem originated in an attempt to construct matrices A with entries 0 and 1 such that the product 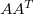 has each entry which is off the main diagonal either 0 or 1.Such matrices are quite common and appear as the incidence matrices of finite projective and affine planes as well as the incidence matrices of configurations such as the Desargues and Pappus configurations.The configurations which we study are all self-dual.The question of whether configurations which admit a preassigned group of collineations can be constructed is also addressed.
has each entry which is off the main diagonal either 0 or 1.Such matrices are quite common and appear as the incidence matrices of finite projective and affine planes as well as the incidence matrices of configurations such as the Desargues and Pappus configurations.The configurations which we study are all self-dual.The question of whether configurations which admit a preassigned group of collineations can be constructed is also addressed.
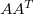 has each entry which is off the main diagonal either 0 or 1.Such matrices are quite common and appear as the incidence matrices of finite projective and affine planes as well as the incidence matrices of configurations such as the Desargues and Pappus configurations.The configurations which we study are all self-dual.The question of whether configurations which admit a preassigned group of collineations can be constructed is also addressed.
has each entry which is off the main diagonal either 0 or 1.Such matrices are quite common and appear as the incidence matrices of finite projective and affine planes as well as the incidence matrices of configurations such as the Desargues and Pappus configurations.The configurations which we study are all self-dual.The question of whether configurations which admit a preassigned group of collineations can be constructed is also addressed.DOI Code:
10.1285/i15900932v7n1p91
Full Text: PDF


