Knots and physics
Abstract
This paper traces the construction of the bracket model of the Jones polynomial, and how this model can be naturally interpreted as a vacuum-vacuum expectation in a combinatorial version of physical theory. From this point of view certain structures such as solutions to the Yang-Baxter equation, and the quantum group for 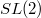 emerge naturally from topological considerations. We then see how quantum groups give rise to invariants of links via solutions to the Yang-Baxter equation. Section 5, is an original treatment of the construction of the universal R-matrix. All the other material has, or will appear elsewhere in similar form.
emerge naturally from topological considerations. We then see how quantum groups give rise to invariants of links via solutions to the Yang-Baxter equation. Section 5, is an original treatment of the construction of the universal R-matrix. All the other material has, or will appear elsewhere in similar form.
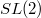 emerge naturally from topological considerations. We then see how quantum groups give rise to invariants of links via solutions to the Yang-Baxter equation. Section 5, is an original treatment of the construction of the universal R-matrix. All the other material has, or will appear elsewhere in similar form.
emerge naturally from topological considerations. We then see how quantum groups give rise to invariants of links via solutions to the Yang-Baxter equation. Section 5, is an original treatment of the construction of the universal R-matrix. All the other material has, or will appear elsewhere in similar form.DOI Code:
10.1285/i15900932v9supp17
Full Text: PDF


