Linear transformation of Tauberian type in normed spaces
Abstract
Let 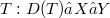 be a linear transformation where X and Y are normed spaces. We call T Tauberian if
be a linear transformation where X and Y are normed spaces. We call T Tauberian if 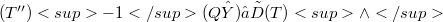 where Q is the quotient map defined on
where Q is the quotient map defined on 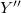 with kernel
with kernel 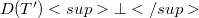 .Bounded Tauberian operators in Banach spaces were studied by Kalton and Wilansky in [KW]. As Gonzalez and Onieva remark in [G03], these operators appear in summability (see [GW]), factorization of operators [DFJP], [N], preservation of isomorphic properties of Banach spaces [N], the preservation of the closed ness of images of closed sets [NR], the equivalence between the Radon-Nikodym property and the Krein-Milman property [S], and generalized Fredholm operators [T], [Y].Classes of Tauberian operators related to a certain measure of weak compactness are investigated in [AT].Other recent works are [AG] (which contains the solution of a problem raised in [KW]), [Gon1], [Gon2], [GO1], [G02], [G03], and [MP].The present paper investigates unbounded Tauberian operators.This wider class is a natural object of study in any investigation concerning the second adjoint
.Bounded Tauberian operators in Banach spaces were studied by Kalton and Wilansky in [KW]. As Gonzalez and Onieva remark in [G03], these operators appear in summability (see [GW]), factorization of operators [DFJP], [N], preservation of isomorphic properties of Banach spaces [N], the preservation of the closed ness of images of closed sets [NR], the equivalence between the Radon-Nikodym property and the Krein-Milman property [S], and generalized Fredholm operators [T], [Y].Classes of Tauberian operators related to a certain measure of weak compactness are investigated in [AT].Other recent works are [AG] (which contains the solution of a problem raised in [KW]), [Gon1], [Gon2], [GO1], [G02], [G03], and [MP].The present paper investigates unbounded Tauberian operators.This wider class is a natural object of study in any investigation concerning the second adjoint 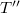 of an unbounded operator, about which little seems to be known.Our main goal is Theorem 3.10 which implies as a corollary the following partial characterization: Let
of an unbounded operator, about which little seems to be known.Our main goal is Theorem 3.10 which implies as a corollary the following partial characterization: Let 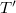 be continuous. Then T is Tauberian if and only if for each bounded subset B of
be continuous. Then T is Tauberian if and only if for each bounded subset B of  , if
, if  is relatively
is relatively 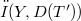 compact (alternatively, relatively
compact (alternatively, relatively 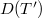 -seminorm compact) then B is relatively
-seminorm compact) then B is relatively 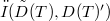 compact.This result contains the well known characterization [KW; Theorem 3.2] for the classical case. Section 4 provides some examples and further properties of Tauberian operators; thus for example the usual closable ordinary differential operators defined between
compact.This result contains the well known characterization [KW; Theorem 3.2] for the classical case. Section 4 provides some examples and further properties of Tauberian operators; thus for example the usual closable ordinary differential operators defined between 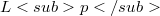 , spaces (see e.g. [Go1; Ch VI]) and their successive adjoints are all Tauberian (Corollaries 4.6 and 4.7). Section 5 looks at the continuous case.
, spaces (see e.g. [Go1; Ch VI]) and their successive adjoints are all Tauberian (Corollaries 4.6 and 4.7). Section 5 looks at the continuous case.
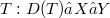 be a linear transformation where X and Y are normed spaces. We call T Tauberian if
be a linear transformation where X and Y are normed spaces. We call T Tauberian if 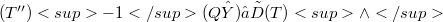 where Q is the quotient map defined on
where Q is the quotient map defined on 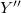 with kernel
with kernel 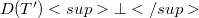 .Bounded Tauberian operators in Banach spaces were studied by Kalton and Wilansky in [KW]. As Gonzalez and Onieva remark in [G03], these operators appear in summability (see [GW]), factorization of operators [DFJP], [N], preservation of isomorphic properties of Banach spaces [N], the preservation of the closed ness of images of closed sets [NR], the equivalence between the Radon-Nikodym property and the Krein-Milman property [S], and generalized Fredholm operators [T], [Y].Classes of Tauberian operators related to a certain measure of weak compactness are investigated in [AT].Other recent works are [AG] (which contains the solution of a problem raised in [KW]), [Gon1], [Gon2], [GO1], [G02], [G03], and [MP].The present paper investigates unbounded Tauberian operators.This wider class is a natural object of study in any investigation concerning the second adjoint
.Bounded Tauberian operators in Banach spaces were studied by Kalton and Wilansky in [KW]. As Gonzalez and Onieva remark in [G03], these operators appear in summability (see [GW]), factorization of operators [DFJP], [N], preservation of isomorphic properties of Banach spaces [N], the preservation of the closed ness of images of closed sets [NR], the equivalence between the Radon-Nikodym property and the Krein-Milman property [S], and generalized Fredholm operators [T], [Y].Classes of Tauberian operators related to a certain measure of weak compactness are investigated in [AT].Other recent works are [AG] (which contains the solution of a problem raised in [KW]), [Gon1], [Gon2], [GO1], [G02], [G03], and [MP].The present paper investigates unbounded Tauberian operators.This wider class is a natural object of study in any investigation concerning the second adjoint 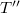 of an unbounded operator, about which little seems to be known.Our main goal is Theorem 3.10 which implies as a corollary the following partial characterization: Let
of an unbounded operator, about which little seems to be known.Our main goal is Theorem 3.10 which implies as a corollary the following partial characterization: Let 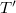 be continuous. Then T is Tauberian if and only if for each bounded subset B of
be continuous. Then T is Tauberian if and only if for each bounded subset B of 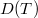 , if
, if 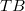 is relatively
is relatively 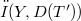 compact (alternatively, relatively
compact (alternatively, relatively 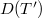 -seminorm compact) then B is relatively
-seminorm compact) then B is relatively 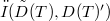 compact.This result contains the well known characterization [KW; Theorem 3.2] for the classical case. Section 4 provides some examples and further properties of Tauberian operators; thus for example the usual closable ordinary differential operators defined between
compact.This result contains the well known characterization [KW; Theorem 3.2] for the classical case. Section 4 provides some examples and further properties of Tauberian operators; thus for example the usual closable ordinary differential operators defined between 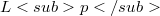 , spaces (see e.g. [Go1; Ch VI]) and their successive adjoints are all Tauberian (Corollaries 4.6 and 4.7). Section 5 looks at the continuous case.
, spaces (see e.g. [Go1; Ch VI]) and their successive adjoints are all Tauberian (Corollaries 4.6 and 4.7). Section 5 looks at the continuous case.DOI Code:
10.1285/i15900932v10supn1p193
Full Text: PDF


