On the fixed points of the Lie algebras associated with a free group presentation
Abstract
Linear methods are an important tool in group theory. A standard procedure is to associate Lie algebras 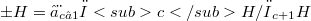 with suitable central subgroup series
with suitable central subgroup series 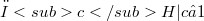 of the group H under consideration.Thus the commutation in groups may be expressed in terms of (bi)linear forms. Conditions of various kinds on the subgroup series lead to different Lie algebra structures.In this paper we are concerned with three types of central subgroup series (two of them being connected with a prime number p), which have the common property that they carry free groups H into free Lie algebras of several type.We prove (Theorems 1 and 2) that for any group G given by a free presentation
of the group H under consideration.Thus the commutation in groups may be expressed in terms of (bi)linear forms. Conditions of various kinds on the subgroup series lead to different Lie algebra structures.In this paper we are concerned with three types of central subgroup series (two of them being connected with a prime number p), which have the common property that they carry free groups H into free Lie algebras of several type.We prove (Theorems 1 and 2) that for any group G given by a free presentation 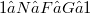 the fixed point subalgebras of the three Lie algebras mentioned form a free subalgebra (G acts on
the fixed point subalgebras of the three Lie algebras mentioned form a free subalgebra (G acts on 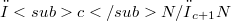 by conjugation). For showing that in the two p-cases we can choose, in fact, the same free generating set we state a more general result (Theorem 5) conceming the fixed points of free restricted Lie algebras with respect to a homogeneous group action which is of independent interest.The centres of the groups
by conjugation). For showing that in the two p-cases we can choose, in fact, the same free generating set we state a more general result (Theorem 5) conceming the fixed points of free restricted Lie algebras with respect to a homogeneous group action which is of independent interest.The centres of the groups 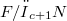 are described (Theorems 3 and 4).
are described (Theorems 3 and 4).
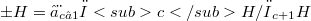 with suitable central subgroup series
with suitable central subgroup series 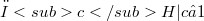 of the group H under consideration.Thus the commutation in groups may be expressed in terms of (bi)linear forms. Conditions of various kinds on the subgroup series lead to different Lie algebra structures.In this paper we are concerned with three types of central subgroup series (two of them being connected with a prime number p), which have the common property that they carry free groups H into free Lie algebras of several type.We prove (Theorems 1 and 2) that for any group G given by a free presentation
of the group H under consideration.Thus the commutation in groups may be expressed in terms of (bi)linear forms. Conditions of various kinds on the subgroup series lead to different Lie algebra structures.In this paper we are concerned with three types of central subgroup series (two of them being connected with a prime number p), which have the common property that they carry free groups H into free Lie algebras of several type.We prove (Theorems 1 and 2) that for any group G given by a free presentation 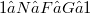 the fixed point subalgebras of the three Lie algebras mentioned form a free subalgebra (G acts on
the fixed point subalgebras of the three Lie algebras mentioned form a free subalgebra (G acts on 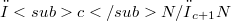 by conjugation). For showing that in the two p-cases we can choose, in fact, the same free generating set we state a more general result (Theorem 5) conceming the fixed points of free restricted Lie algebras with respect to a homogeneous group action which is of independent interest.The centres of the groups
by conjugation). For showing that in the two p-cases we can choose, in fact, the same free generating set we state a more general result (Theorem 5) conceming the fixed points of free restricted Lie algebras with respect to a homogeneous group action which is of independent interest.The centres of the groups 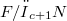 are described (Theorems 3 and 4).
are described (Theorems 3 and 4).DOI Code:
10.1285/i15900932v10n2p235
Full Text: PDF


