On basic sequences in Banach spaces
Abstract
Let X be a Banach space with 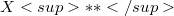 separable. If X has a shrinking basis and Y is a closed subspace of
separable. If X has a shrinking basis and Y is a closed subspace of 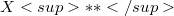 which contains X, there exists a shrinking basis
which contains X, there exists a shrinking basis 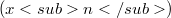 in X with two complementary subsequences
in X with two complementary subsequences 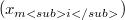 and
and 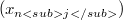 so that
so that ![[x_{m<sub>j</sub>}]](http://212.189.136.205/plugins/generic/latexRender/cache/f1ce0d91842a11df6d8ddebf158be264.png) is a reflexive space and
is a reflexive space and ![X +[\widetilde{x_{n<sub>j</sub>}}]= Y](http://212.189.136.205/plugins/generic/latexRender/cache/b5bd32e4e3f113ffcd56a0a047d15551.png) , where we are denoting by
, where we are denoting by ![[\widetilde{x_{n<sub>j</sub>}}]](http://212.189.136.205/plugins/generic/latexRender/cache/f44530db2352e12c1f8e9bbda57cfbc1.png) the weak-star closure of
the weak-star closure of ![[x_{n<sub>j</sub>}]](http://212.189.136.205/plugins/generic/latexRender/cache/2599d2644c7e374f98aa7b6e7d716aa4.png) in
in 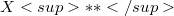 . If
. If 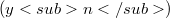 is a sequence in X that converges to a point in
is a sequence in X that converges to a point in 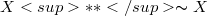 for the weak-star topology,there is a basic sequence
for the weak-star topology,there is a basic sequence 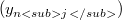 in
in 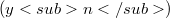 such that
such that ![[y_{n<sub>j</sub>}]](http://212.189.136.205/plugins/generic/latexRender/cache/1ea11f01e20b017e70d9904d880c136b.png) is a quasi-reflexive Banach space of order one. Given a Banach space Z with basis it is also proved that every basic sequence
is a quasi-reflexive Banach space of order one. Given a Banach space Z with basis it is also proved that every basic sequence 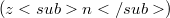 in Z has a subsequence extending to a basis of Z.
in Z has a subsequence extending to a basis of Z.
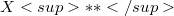 separable. If X has a shrinking basis and Y is a closed subspace of
separable. If X has a shrinking basis and Y is a closed subspace of 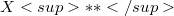 which contains X, there exists a shrinking basis
which contains X, there exists a shrinking basis 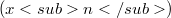 in X with two complementary subsequences
in X with two complementary subsequences 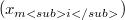 and
and 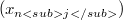 so that
so that ![[x_{m<sub>j</sub>}]](http://212.189.136.205/plugins/generic/latexRender/cache/f1ce0d91842a11df6d8ddebf158be264.png) is a reflexive space and
is a reflexive space and ![X +[\widetilde{x_{n<sub>j</sub>}}]= Y](http://212.189.136.205/plugins/generic/latexRender/cache/b5bd32e4e3f113ffcd56a0a047d15551.png) , where we are denoting by
, where we are denoting by ![[\widetilde{x_{n<sub>j</sub>}}]](http://212.189.136.205/plugins/generic/latexRender/cache/f44530db2352e12c1f8e9bbda57cfbc1.png) the weak-star closure of
the weak-star closure of ![[x_{n<sub>j</sub>}]](http://212.189.136.205/plugins/generic/latexRender/cache/2599d2644c7e374f98aa7b6e7d716aa4.png) in
in 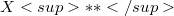 . If
. If 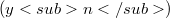 is a sequence in X that converges to a point in
is a sequence in X that converges to a point in 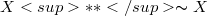 for the weak-star topology,there is a basic sequence
for the weak-star topology,there is a basic sequence 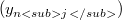 in
in 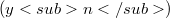 such that
such that ![[y_{n<sub>j</sub>}]](http://212.189.136.205/plugins/generic/latexRender/cache/1ea11f01e20b017e70d9904d880c136b.png) is a quasi-reflexive Banach space of order one. Given a Banach space Z with basis it is also proved that every basic sequence
is a quasi-reflexive Banach space of order one. Given a Banach space Z with basis it is also proved that every basic sequence 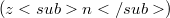 in Z has a subsequence extending to a basis of Z.
in Z has a subsequence extending to a basis of Z.DOI Code:
10.1285/i15900932v12p245
Full Text: PDF


