Maximal sector of analyticity for 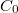 -semigroups generated by elliptic operators with separation property in
-semigroups generated by elliptic operators with separation property in 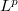
Abstract
Analytic continuation of the 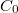 -semigroup
-semigroup 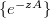 on
on 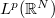 generated by the second order elliptic operator
generated by the second order elliptic operator 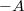 is investigated, where
is investigated, where 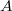 is formally defined by the differential expression
is formally defined by the differential expression 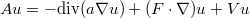 and the lower order coefficients have singularities at infinity or at the origin. \end
and the lower order coefficients have singularities at infinity or at the origin. \end
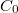 -semigroup
-semigroup 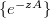 on
on 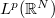 generated by the second order elliptic operator
generated by the second order elliptic operator 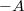 is investigated, where
is investigated, where 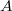 is formally defined by the differential expression
is formally defined by the differential expression 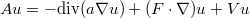 and the lower order coefficients have singularities at infinity or at the origin. \end
and the lower order coefficients have singularities at infinity or at the origin. \endDOI Code:
10.1285/i15900932v33n2p65
Keywords:
Second order linear elliptic operators in $L^{p}$; analytic $C_{0}$-semigroups; maximal sectors of analyticity
Full Text: PDF


