Weak closures and derived sets in dual Banach spaces
closures and derived sets in dual Banach spaces
Abstract
The main results of the paper: \textbf{(1)} The dual Banach space 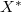 contains a linear subspace
contains a linear subspace 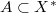 such that the set
such that the set 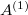 of all limits of weak
of all limits of weak convergent bounded nets in
convergent bounded nets in 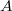 is a proper norm-dense subset of
is a proper norm-dense subset of 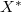 if and only if
if and only if 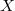 is a non-quasi-reflexive Banach space containing an infinite-dimensional subspace with separable dual. \textbf{(2)} Let
is a non-quasi-reflexive Banach space containing an infinite-dimensional subspace with separable dual. \textbf{(2)} Let 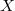 be a non-reflexive Banach space. Then there exists a convex subset
be a non-reflexive Banach space. Then there exists a convex subset 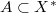 such that
such that 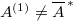 (the latter denotes the weak
(the latter denotes the weak closure of
closure of 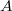 ). \textbf{(3)} Let
). \textbf{(3)} Let 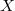 be a quasi-reflexive Banach space and
be a quasi-reflexive Banach space and 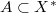 be an absolutely convex subset. Then
be an absolutely convex subset. Then 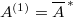 .
.
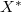 contains a linear subspace
contains a linear subspace 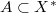 such that the set
such that the set 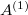 of all limits of weak
of all limits of weak convergent bounded nets in
convergent bounded nets in 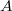 is a proper norm-dense subset of
is a proper norm-dense subset of 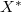 if and only if
if and only if 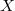 is a non-quasi-reflexive Banach space containing an infinite-dimensional subspace with separable dual. \textbf{(2)} Let
is a non-quasi-reflexive Banach space containing an infinite-dimensional subspace with separable dual. \textbf{(2)} Let 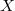 be a non-reflexive Banach space. Then there exists a convex subset
be a non-reflexive Banach space. Then there exists a convex subset 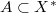 such that
such that 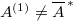 (the latter denotes the weak
(the latter denotes the weak closure of
closure of 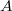 ). \textbf{(3)} Let
). \textbf{(3)} Let 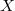 be a quasi-reflexive Banach space and
be a quasi-reflexive Banach space and 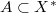 be an absolutely convex subset. Then
be an absolutely convex subset. Then 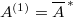 .
.DOI Code:
10.1285/i15900932v31n1p129
Keywords:
norming subspace ; quasi-reflexive Banach space ; total subspace ; weak$^*$ closure ; weak$^*$ derived set ; weak$^*$ sequential closure
Full Text: PDF


