A comparison study between three different Kernel estimators for the Hazard rate function

Abstract

Kernel estimation is one of the most important data analytical tool, if we consider the non parametric approach in the estimation of the probability density function. In parallel, its used to estimate the hazard rate function, which is one of the  most important ways for representing the life time distribution in the survival analysis. 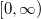As the support of the hazard rate function is in the non negative part of the real line , its will be under the boundary effect near zero when the estimation is done using symmetric kernels such as the Gaussian kernel. Two kernel estimators for the hazard rate function were proposed using asymmetric kernels are the Reciprocal Inverse Gaussian and Inverse Gaussian kernel estimators to avoid the high bias near zero. In this paper, we propose a theoretical comparison between those estimators by looking at their asymptotic bias, variance and the mean squared error. Also, a comparison of the practical performance of the two estimators based on simulated and real data will be present.