A Simple and Conservative Empirical Likelihood Function--Corrected
Abstract
The likelihood function
![L(\mu) = \left[1 +N\left((\mu-\overline{x})) / s \right)^2 \right]^{-n/2}](http://212.189.136.205/plugins/generic/latexRender/cache/4573eca6c92350ed4327144bb2a65f5c.png) is derived,
is derived,
where 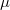 is the true value,
is the true value, 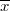 is the mean,
is the mean,
and 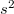 is the variance of
is the variance of 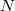 measurements. This form approaches a normal for
measurements. This form approaches a normal for 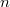 large, but can be used also for
large, but can be used also for 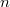 small.
small.
The use of this formula in data modeling is discussed.
DOI Code:
10.1285/i20705948v8n2p267
Keywords:
likelihood function; empirical; data analysis; lognormal; probabilistic; Bayesian
References
%ARTICLE:
bibitem[Miller, 2014]{Miller2014}
Miller, Guthrie (2014).
newblock A Simple and Conservative Empirical Likelihood Function.
newblock {em Electronic Journal of Applied Statistical Analysis}, 7(2), pages 344--349. (2014).
%BOOK
bibitem[Miller, 2015]{Miller2015}
Miller, Guthrie (2015).
newblock {em Probabilistic Interpretation of Data--A Physicist's Approach}.
newblock Lulu Publications.
Full Text: pdf


